刷题日记——每日一题
前言:
突然心血来潮开拓一个刷题日记的版块,这个板块主要是一些个人算法算题的笔记和一些个人心得。
其实最初激励我接触到博客的就是在洛谷平台刷题的时候,里面社区激烈的讨论氛围,所以我的第一篇博客就是写的刷题心得分享
如果你打开友链中博主的老博客,你会发现我之前大多数的帖子也是刷题的算法分享。
现在一方面打算回归初心继续开始每日刷题,一方面发现自己最近过于依赖ai,coding能力直线下滑,于是打算借由刷题的契机重新锻炼coding能力
每日私货

刷题日记记录规则纲要
- 该板块将会记录包括但不限于洛谷,leetcode,牛客,codeforces等等刷题平台的题
- 该板块不会记流水账一样记录一些过于简单的题,但是会记录经典算法的模板或是综合难题
25.9.6 3495.使数组元素都变为零的最少操作次数
题目描述
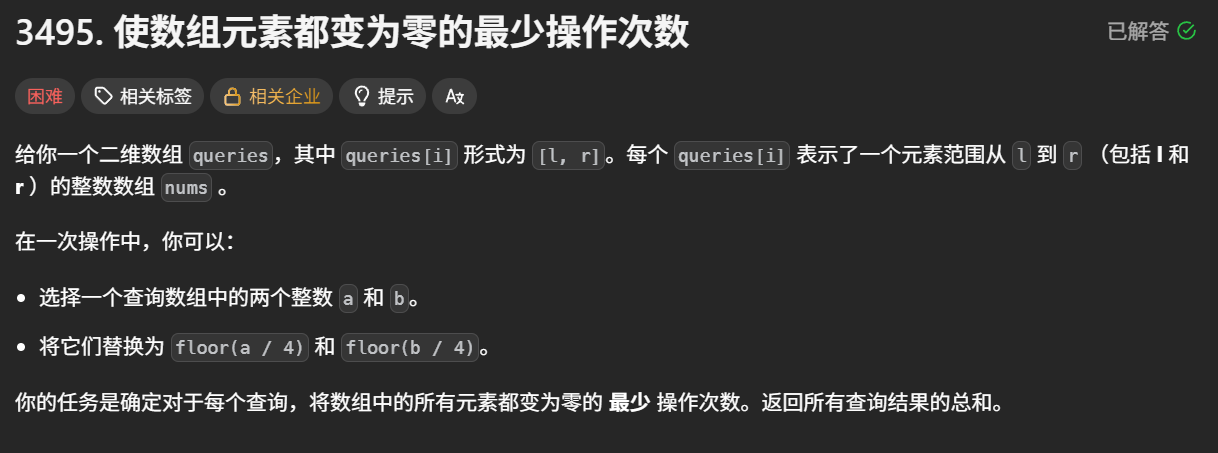
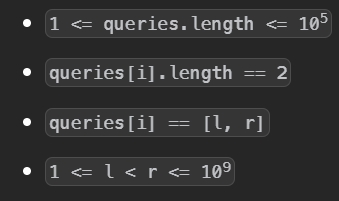
数据范围:
解题思路
1.大致方向确定
按照以往算题的经验,我们读完题之后,先研究数据范围
正常评测1s支持的操作次数在1e8数量级,这里查询次数就是1e5数量级,也就是说我们每次查询的开销要压缩进1e3数量级
同时我们发现每次查询它只给出起始和终止的范围,而这个范围最大为1e9数量级,如果O(N)遍历显然是不现实的,所以我们合理猜猜我们需要使用log(N)复杂度的处理方式完成每次查询,而和数相关的log(N)的处理方式显然就是按进制处理,比如$log_2(1e9)$也不过三十几。
2.题目要求简化
在确认好每次查询我们需要按二进制或者四进制位遍历的大致方向之后,我们开始明确细节
题目是给我们一个[L, R] ,代表我们需要将从L到R的所有整数,每次操作选两个数除以4,向下取整。要求使得所有数为零的最小操作数,这里其实存在一个陷阱,最小操作数?这让我们下意识警觉到难道每次选哪两个数还有策略吗?但是其实非也
不难证明我们每次只要选择数组中任意两个非零的整数进行除以4的操作,其操作都是等效的,所以其中我们操作的顺序是没有要求的,所以我们不妨将这个数组视为一个整体,每个数到0所需的除以4的次数我们定义为每个数所需的操作数,我们可以将这个数组所有数的所需的操作数加起来,而每次操作可以除以两次4,即等效为我们每次可以消耗2个操作次数
所以这个数组的所需的操作数即为:
Y=(\sum_{i=L}^R(P_i)+1)//2这里 Y 即为所需的操作数, $ P_{i} $代表每个数所需的操作数,+1是为了向上取整
但是上面这个公式有个问题,由于
P_{i} = log_{4}(i)+1
上面的公式进一步推导为:
原式展开:
Y = \tfrac{1}{2} \left( \sum_{i=L}^R \log_{4}(i) + (R-L+1) + 1 \right)
底数转化:
由于$\log_{4}(i) = \frac{\ln i}{\ln 4}$ ,所以可得
\sum_{i=L}^R \log_{4}(i) = \frac{1}{\ln 4} \sum_{i=L}^R \ln i
求和消除:
由于求和这里没有明显规律,如果遍历求解时间复杂度显然不可接受,这里我们将求和在对数函数的范畴转为阶乘
\sum_{i=L}^R \ln i = \ln \left( \prod_{i=L}^R i \right) = \ln \left(\frac{R!}{(L-1)!} \right)
最终推导式:
Y = \tfrac{1}{2} \left( \frac{\log_4 {(R!)}}{\log_4((L-1)!)} + (R-L+2)\right)
最后我们又发现 其实$log_{4}(k!)$求解其实是有规律的
| 每个数所需操作数 | 该区间数的总数 | |
|---|---|---|
| [1, 3] | 1 | 3 |
| [4, 15] | 2 | $ 3*4^{(2-1)} $ |
| [16, 63] | 3 | $ 3*4^{(3-1)} $ |
| $ [4^{i}, 4^{i+1}-1] $ | i+1 | $ 3*4^i $ |
由上我们不妨将$ log_{4}(k!) $写成一个get函数
代码展示
由上的解题思路,我们不难得到下面的代码
class Solution(object):
# 获取
def get(self, num):
count_base = 3
base1 = 1
base = 1
ans = 0
while base<=num:
if(base*4-1<=num):
ans+=(base1)*count_base
else: # 注意边界控制
ans+=(base1)*(num-base+1)
base*=4
base1+=1
count_base*=4
return ans
def minOperations(self, queries):
"""
:type queries: List[List[int]]
:rtype: int
"""
ans = 0
for query in queries:
count = self.get(query[1])-self.get(query[0]-1)
ans += (count+1)//2
return ans
结果
进一步优化
由上面的代码我们其实发现还能再合理处理范围再凹一凹我们的极限优化一下
上面我们将求解$log{4}((L-1)!)$和$log{4}(R!)$是分开处理的,但是实际上我们在处理后者的途中可以顺带将前者也计算出来:
优化代码:
class Solution(object):
def get(self, num):
count_base = 3
base1 = 1
base = 1
ans = 0
while base<=num:
if(base*4-1<=num):
ans+=(base1)*count_base
else:
ans+=(base1)*(num-base+1)
base*=4
base1+=1
count_base*=4
return ans
def get1(self, num1, num2):
count_base = 3
base1 = 1
base = 1
ans = 0
ans1 = 0
flag = 0
while base<=num2:
if(base*4-1<=num2):
ans+=(base1)*count_base
else:
ans+=(base1)*(num2-base+1)
if(base*4-1<=num1):
ans1+=(base1)*count_base
elif(flag == 0):
ans1+=base1*(num1-base+1)
flag = 1
base*=4
base1+=1
count_base*=4
return ans-ans1
def minOperations(self, queries):
"""
:type queries: List[List[int]]
:rtype: int
"""
ans = 0
for query in queries:
# count = self.get(query[1])-self.get(query[0]-1)
count = self.get1(query[0]-1, query[1])
ans += (count+1)//2
return ans
优化结果:
在评论区我还发现了提前打表,计算查表的邪修做法,可谓是大开眼界了,感兴趣的同学可以去自行了解一下~

